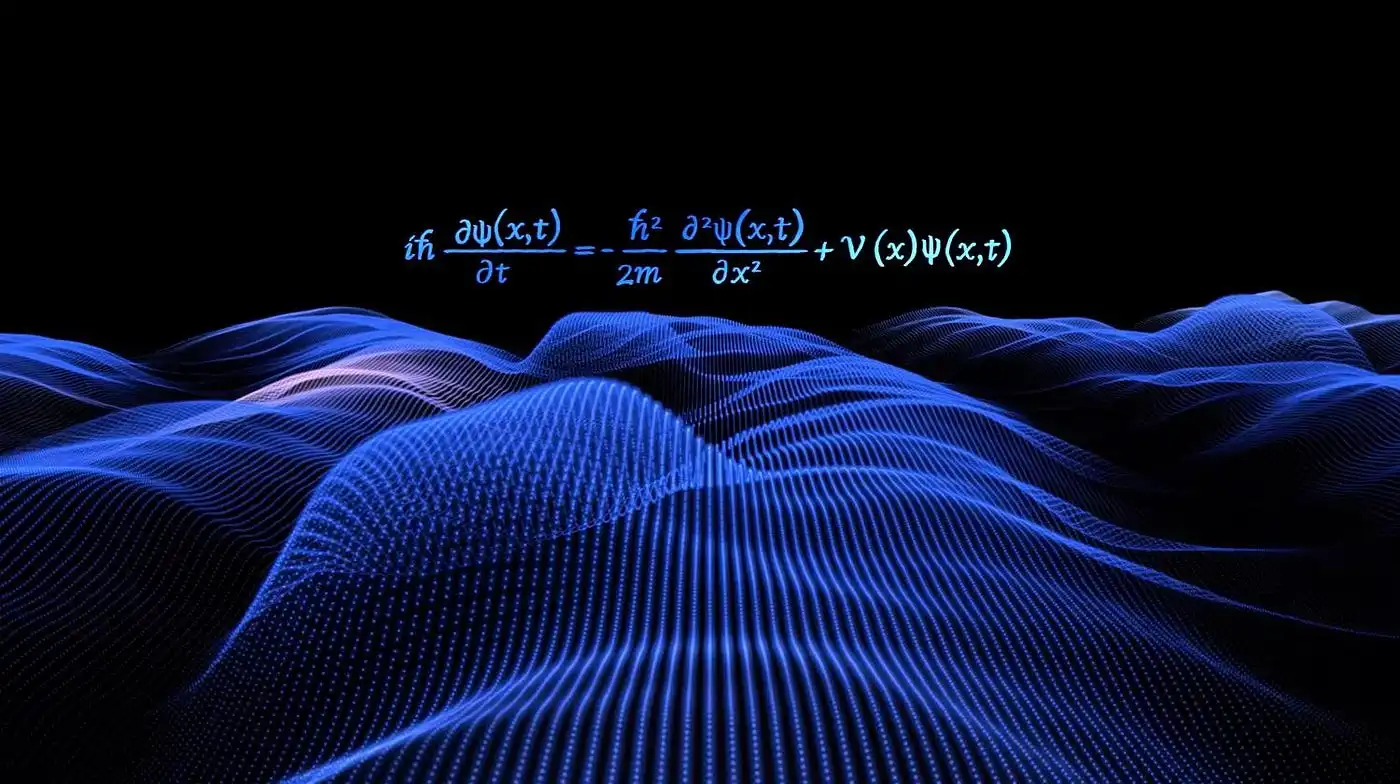
Schrödinger Equation for Multi-Electron Systems

The Schrödinger equation is a cornerstone of quantum mechanics, providing a mathematical framework to describe the behavior of particles at the atomic and subatomic levels. When applied to multi-electron systems, however, the equation becomes significantly more complex due to electron-electron interactions and the many-body nature of the problem. 

In this article, we’ll explore the challenges, approximations, and computational methods used to solve the Schrödinger equation for systems with multiple electrons.

What Is the Schrödinger Equation?

At its core, the Schrödinger equation is used to predict how quantum systems evolve over time. In its time-independent form, the equation is written as:

$hat{H}Psi = EPsi$

Here, $hat{H}$ is the Hamiltonian operator representing the total energy of the system, $Psi$ is the wavefunction, and $E$ is the energy eigenvalue. For a single electron moving in a potential, this equation can be solved exactly under certain conditions. However, as soon as more electrons are introduced, the complexity increases dramatically.

Challenges in Multi-Electron Systems

Electron-Electron Interactions

In multi-electron systems, each electron experiences not only the attractive force from the nucleus but also repulsive forces from all other electrons. This electron-electron interaction adds extra terms to the Hamiltonian, making the equation much more challenging to solve exactly.

Many-Body Problem

The presence of multiple electrons turns the problem into a many-body problem. The exact solution of the Schrödinger equation for many interacting particles is computationally intractable for all but the simplest systems. As a result, scientists rely on approximation methods and computational techniques to model these systems.

Approximations and Computational Methods

To deal with the complexity of multi-electron systems, several methods have been developed:

1. Hartree-Fock Method

The Hartree-Fock method is one of the most widely used approximations in quantum chemistry. It simplifies the problem by assuming that each electron moves independently in an average field created by all other electrons. This method replaces the many-body wavefunction with a single Slater determinant, providing a starting point for more sophisticated techniques.

2. Post-Hartree-Fock Methods

To account for electron correlation—interactions that the Hartree-Fock method may overlook—post-Hartree-Fock methods are used. Techniques such as Configuration Interaction (CI), Møller-Plesset perturbation theory (MPn), and Coupled Cluster (CC) methods systematically improve upon the Hartree-Fock approximation to yield more accurate results.

3. Density Functional Theory (DFT)

Density Functional Theory has become popular due to its balance between computational efficiency and accuracy. DFT transforms the many-body problem into a functional of the electron density, bypassing the need for a complex many-electron wavefunction. This approach is especially useful for studying large molecules and solid-state systems.

Applications of Multi-Electron Schrödinger Equation Solutions

Understanding the Schrödinger equation for multi-electron systems is crucial for various fields:

• Quantum Chemistry: Accurate modeling of chemical reactions, bonding, and molecular structure.

• Material Science: Predicting the electronic properties of materials, which is key to developing new technologies.

• Nanotechnology: Designing and optimizing nanoscale devices by understanding electron behavior at the quantum level.

• Computational Physics: Advancing simulation techniques that can predict complex quantum phenomena.

Conclusion

The Schrödinger equation for multi-electron systems remains one of the most challenging and fascinating areas in quantum mechanics. While the exact solution is often unattainable due to the complexity introduced by electron-electron interactions and the many-body problem, approximation methods such as Hartree-Fock, post-Hartree-Fock techniques, and Density Functional Theory provide valuable insights. These methods have revolutionized fields like quantum chemistry, material science, and nanotechnology, paving the way for innovative technologies and a deeper understanding of the quantum world.